Предисловие
Человек проявляет интерес к многогранникам на протяжении всей своей сознательной деятельности — от двухлетнего ребёнка, играющего деревянными кубиками, до зрелого математика, наслаждающегося чтением книги Бранко Грюнбаума «Выпуклые многогранники» [11]. Некоторые из правильных и полуправильных тел встречаются в природе в виде кристаллов, другие — в виде вирусов (которые можно рассмотреть с помощью электронного микроскопа). Пчёлы строили шестиугольные соты задолго до появления человека, а в истории цивилизации создание многогранных тел (подобных пирамидам) наряду с другими видами пластических искусств уходит в глубь веков. Пять правильных тел изучали Теэтет, Платон, Евклид, Гипсикл и Папп.
Значительная часть этой книги посвящена однородным многогранникам, грани которых — правильные многоугольники — вблизи любой вершины расположены в одном порядке. (Такой многогранник называется правильным, если все ограничивающие его многоугольники одинаковы.) Согласно теореме Евклида, применимой ко всем выпуклым многогранным углам, в любом из них сумма плоских углов при вершине меньше 360°. Изготовив самостоятельно несколько моделей, читатель заметит, что разность между 360° и этой суммой для одних тел может оказаться значительной (так, у куба, который имеет 8 многогранных углов, для каждого угла рассматриваемая разность составляет 90°), а для других, у которых многогранных углов больше, разность окажется гораздо меньшей (так, для курносого1 додекаэдра, имеющего 60 углов, она равна всего 12°). Подобные наблюдения привели Рене Декарта (1596—1650) к открытию и доказательству теоремы, утверждающей, что сумма всех таких разностей (математики называют их угловыми дефектами) неизменно равна 720°2.
 Приблизительно в это же время Иоганн Кеплер (1571—1630) написал этюд «О снежинке», в котором высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных — куб, а его, если позволительно так сказать, супруга — октаэдр, ибо у октаэдра столько углов, сколь у куба граней». Кеплер первым опубликовал полный список тринадцати архимедовых тел и дал им те названия, под которыми они известны поныне. (Труд самого Архимеда утрачен; как полагают, его рукопись погибла во время знаменитого пожара Александрийской библиотеки, столь едко описанного в пьесе Бернарда Шоу «Цезарь и Клеопатра».) Кеплеру же принадлежит заслуга в постановке проблемы перечисления изозоноэдров (выпуклых многогранников, грани которых суть равные ромбы); он также внёс первый вклад в её решение, открыв ромбододекаэдр и триаконтаэдр. Однако с позиций этой книги, пожалуй, наиболее существенный вклад Кеплера в теорию многогранников заключался в предложении рассматривать невыпуклые многогранники со звёздчатыми гранями, подобными пентаграмме
. По всей вероятности, Кеплер не подозревал о существовании более ранней работы Томаса Бредвердайна (1290—1349) (ставшего архиепископом Кентерберийским3 в последний месяц своей жизни), посвящённой звёздчатым многоугольникам.
Приблизительно в это же время Иоганн Кеплер (1571—1630) написал этюд «О снежинке», в котором высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных — куб, а его, если позволительно так сказать, супруга — октаэдр, ибо у октаэдра столько углов, сколь у куба граней». Кеплер первым опубликовал полный список тринадцати архимедовых тел и дал им те названия, под которыми они известны поныне. (Труд самого Архимеда утрачен; как полагают, его рукопись погибла во время знаменитого пожара Александрийской библиотеки, столь едко описанного в пьесе Бернарда Шоу «Цезарь и Клеопатра».) Кеплеру же принадлежит заслуга в постановке проблемы перечисления изозоноэдров (выпуклых многогранников, грани которых суть равные ромбы); он также внёс первый вклад в её решение, открыв ромбододекаэдр и триаконтаэдр. Однако с позиций этой книги, пожалуй, наиболее существенный вклад Кеплера в теорию многогранников заключался в предложении рассматривать невыпуклые многогранники со звёздчатыми гранями, подобными пентаграмме
. По всей вероятности, Кеплер не подозревал о существовании более ранней работы Томаса Бредвердайна (1290—1349) (ставшего архиепископом Кентерберийским3 в последний месяц своей жизни), посвящённой звёздчатым многоугольникам.
В знаменитом соборе в Солсбери столько интересных реликвий, что лишь немногие посетители бросят взгляд на надгробие Томаса Горджеса, усопшего в 1610 году. А между тем резьба на могильном камне содержит изображения додекаэдра, трёх икосаэдров и двух кубооктаэдров. На камне вырезаны скелетные каркасы этих тел в манере, близкой к использованной Леонардо да Винчи при построении моделей однородных многогранников с каркасом из прутьев.
Несколькими милями к юго-западу расположена деревушка Уимборн Сент-Джилс, где в 1627 году был похоронен Энтони Эшли. Его надгробие украшает усечённый икосаэдр, причём изображён не каркас, а сам многогранник, подобный модели 9 этой книги.
Со времён Декарта многие великие математики также уделяли внимание нашей теме. Эйлер открыл и доказал знаменитую формулу
В — Р + Г = 2,
связывающую числа вершин, рёбер и граней любого выпуклого многогранника4. Гаусс применил неправильную сферическую пентаграмму (его pentagramma mirificum) к объяснению правил Напье из сферической тригонометрии. Коши доказал, что всякий выпуклый многогранник с жёсткими гранями, шарнирно соединёнными в рёбрах, остается тем не менее твёрдым телом. Гамильтон придумал икосаэдральную игру5. Фон Штаудт дал новое доказательство формулы Эйлера. Шлефли распространил этот результат на случай n измерений. Большое влияние имела книга Клейна «Лекции об икосаэдре»6. Е. С. Фёдоров продолжил исследование Кеплера по проблеме изозоноэдров, обнаружив весьма необычный, как бы сплющенный ромбоикосаэдр. И наконец, совсем недавно, в 1960 году, Билински завершил перечисление этих тел открытием ещё одного ромбододекаэдра, причём этот последний можно поместить в ящик с измерениями 1, τ и τ2
(где через τ обозначено число (√5+1)/2, выражающее знаменитую «божественную пропорцию», или «золотое сечение»).
Автор этой книги, заражая своим энтузиазмом читателя, дает ему ясные и чёткие указания о том, как изготовить модели различных многогранников. Объяснения проиллюстрированы фотографиями моделей из собрания автора — возможно, наиболее полного в настоящее время. Но фотографии не в состоянии передать всего великолепия самих моделей. Наиболее сложные «курносые» модели не только крайне трудны в изготовлении, но и весьма декоративны. Это ли не превосходный пример родства истины и красоты!
Г. С. М. Кокстер
1
В отечественной литературе соответствующие многогранники часто называются «плосконосыми», однако нам кажется более правильным переводить английский термин snub как «курносый».
2
Это наблюдение привело его также к установлению известного соотношения между числами вершин, рёбер и граней выпуклого много-гранника, сегодня обычно называемого теоремой Эйлера.
3 Главой англиканской церкви.
4
Эта формула доказывается в большом числе научных и научно-популярных сочинений, среди которых, наряду с учебниками [l] и [2], статьёй [3]. пособиями [4], [8] и монографией [5], уместно упомянуть следующие: Д. П о й а, Математическое открытие, М., изд-во «Наука», 1970, гл. 15; И. Л а к а т о с, Доказательства и опровержения. М., изд-во «Наука», 1967.
5
См. § 5 гл. II рассчитанной на учащихся средних школ книги О. О р е, Графы и их применение, М.. изд-во «Мир», 1965.
6
К l e i n F., Vorlesungen über das Ikosaeder und die Auflössung der Gleichungen vom fünften Grade, Leipzig, Teubner, 1884; последнее (английское) издание: К l e i n F., The Icosahedron and the Solution of Equations of the Fifth Degree, N. Y., Dover Publ., 1956. В этой книге Феликс Клейн использует специфические свойства симметрии икосаэдра для доказательства неразрешимости в радикалах уравнений степени n 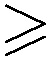 5 (то есть того, чтобы установить отсутствие общей формулы, выражающей корни уравнения
a0xn
+
a1xn
−1
+ ... +
an
−1x
+
an
= 0, где n
5 (то есть того, чтобы установить отсутствие общей формулы, выражающей корни уравнения
a0xn
+
a1xn
−1
+ ... +
an
−1x
+
an
= 0, где n 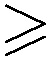 5, через его коэффициенты!). Коротко об этом рассказывается и в книге К л е й н Ф., Элементарная математика с точки зрения высшей, т. I, М.—Л., ОНТИ, 1935, стр. 182—237.
5, через его коэффициенты!). Коротко об этом рассказывается и в книге К л е й н Ф., Элементарная математика с точки зрения высшей, т. I, М.—Л., ОНТИ, 1935, стр. 182—237.
<—
Содержание
—>

 Приблизительно в это же время Иоганн Кеплер (1571—1630) написал этюд «О снежинке», в котором высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных — куб, а его, если позволительно так сказать, супруга — октаэдр, ибо у октаэдра столько углов, сколь у куба граней». Кеплер первым опубликовал полный список тринадцати архимедовых тел и дал им те названия, под которыми они известны поныне. (Труд самого Архимеда утрачен; как полагают, его рукопись погибла во время знаменитого пожара Александрийской библиотеки, столь едко описанного в пьесе Бернарда Шоу «Цезарь и Клеопатра».) Кеплеру же принадлежит заслуга в постановке проблемы перечисления изозоноэдров (выпуклых многогранников, грани которых суть равные ромбы); он также внёс первый вклад в её решение, открыв ромбододекаэдр и триаконтаэдр. Однако с позиций этой книги, пожалуй, наиболее существенный вклад Кеплера в теорию многогранников заключался в предложении рассматривать невыпуклые многогранники со звёздчатыми гранями, подобными пентаграмме
. По всей вероятности, Кеплер не подозревал о существовании более ранней работы Томаса Бредвердайна (1290—1349) (ставшего архиепископом Кентерберийским3 в последний месяц своей жизни), посвящённой звёздчатым многоугольникам.
Приблизительно в это же время Иоганн Кеплер (1571—1630) написал этюд «О снежинке», в котором высказал такое замечание: «Среди правильных тел самое первое, начало и родитель остальных — куб, а его, если позволительно так сказать, супруга — октаэдр, ибо у октаэдра столько углов, сколь у куба граней». Кеплер первым опубликовал полный список тринадцати архимедовых тел и дал им те названия, под которыми они известны поныне. (Труд самого Архимеда утрачен; как полагают, его рукопись погибла во время знаменитого пожара Александрийской библиотеки, столь едко описанного в пьесе Бернарда Шоу «Цезарь и Клеопатра».) Кеплеру же принадлежит заслуга в постановке проблемы перечисления изозоноэдров (выпуклых многогранников, грани которых суть равные ромбы); он также внёс первый вклад в её решение, открыв ромбододекаэдр и триаконтаэдр. Однако с позиций этой книги, пожалуй, наиболее существенный вклад Кеплера в теорию многогранников заключался в предложении рассматривать невыпуклые многогранники со звёздчатыми гранями, подобными пентаграмме
. По всей вероятности, Кеплер не подозревал о существовании более ранней работы Томаса Бредвердайна (1290—1349) (ставшего архиепископом Кентерберийским3 в последний месяц своей жизни), посвящённой звёздчатым многоугольникам.