Замечания о звёздчатых формах и соединениях платоновых тел
Термин «звёздчатый» имеет общий корень со словом «звезда», и это указывает на его происхождение. Существуют звездчатые многоугольники и звездчатые многогранники. Чтобы разобраться в существе дела, обратимся к чертежам и моделям.
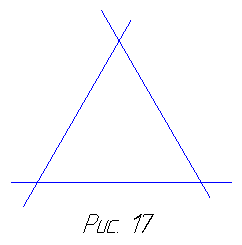
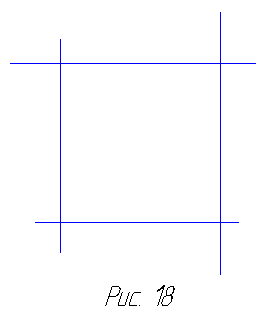 Начнём с простейшего многоугольника — равностороннего треугольника. Посмотрим, что произойдёт, если мы продолжим все три его стороны. Легко заметить, что этими прямыми не будет ограничена никакая новая часть плоскости: продолжения сторон будут р а с х о д и т ь с я (рис. 17). Аналогичная картина предстанет перед нами и в том случае, если мы попытаемся продолжить стороны квадрата. Построенные прямые будут попарно параллельны и не пересекутся, сколько бы их ни продолжали (рис. 18). Тем самым они не добавят никаких новых ограниченных частей плоскости к внутренности квадрата. Однако в случае пятиугольника картина меняется. Продолжения сторон пятиугольника пересекаются во внешней по отношению к пятиугольнику части плоскости, добавляя к пятиугольнику новые части. В результате получается хорошо известная нам пятиконечная звезда, иначе называемая пентаграммой (рис. 19). Пентаграмма была известна в
Начнём с простейшего многоугольника — равностороннего треугольника. Посмотрим, что произойдёт, если мы продолжим все три его стороны. Легко заметить, что этими прямыми не будет ограничена никакая новая часть плоскости: продолжения сторон будут р а с х о д и т ь с я (рис. 17). Аналогичная картина предстанет перед нами и в том случае, если мы попытаемся продолжить стороны квадрата. Построенные прямые будут попарно параллельны и не пересекутся, сколько бы их ни продолжали (рис. 18). Тем самым они не добавят никаких новых ограниченных частей плоскости к внутренности квадрата. Однако в случае пятиугольника картина меняется. Продолжения сторон пятиугольника пересекаются во внешней по отношению к пятиугольнику части плоскости, добавляя к пятиугольнику новые части. В результате получается хорошо известная нам пятиконечная звезда, иначе называемая пентаграммой (рис. 19). Пентаграмма была известна в 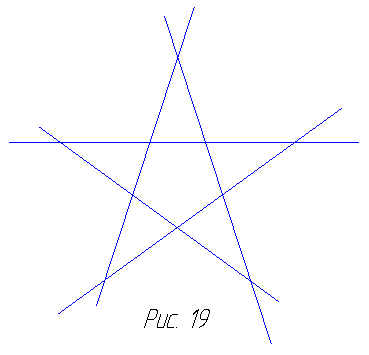 глубокой древности, что явствует хотя бы из того, что пифагорейцы считали её символом здоровья. Продолжение сторон шестиугольника приводит к появлению шестиугольной звезды, или гексаграммы (последнюю можно рассматривать не как единый многоугольник, а как соединение двух равносторонних треугольников).
глубокой древности, что явствует хотя бы из того, что пифагорейцы считали её символом здоровья. Продолжение сторон шестиугольника приводит к появлению шестиугольной звезды, или гексаграммы (последнюю можно рассматривать не как единый многоугольник, а как соединение двух равносторонних треугольников).
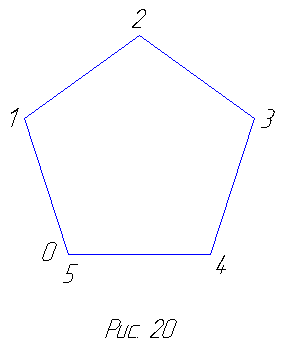 Аналогично правильный восьмиугольник (октагон) приводит нас к восьмиугольной звезде — октаграмме, правильный десятиугольник (декагон) — к десятиугольной звезде, или декаграмме. Пентаграмму, октаграмму и декаграмму можно рассматривать как нераспадающиеся единые многоугольники соответственно с 5, 8 и 10 сторонами, поскольку существует непрерывный обход их вершин по сторонам вокруг центров. При этом в случае пентаграммы, например, совершая полный обход в порядке, определяемом номерами 0-5 (рис. 21), мы делаем два оборота вокруг центра пентаграммы, тогда как при обходе пятиугольника (рис. 20) мы делаем лишь один оборот. В случае же октаграммы и декаграммы получается по три
Аналогично правильный восьмиугольник (октагон) приводит нас к восьмиугольной звезде — октаграмме, правильный десятиугольник (декагон) — к десятиугольной звезде, или декаграмме. Пентаграмму, октаграмму и декаграмму можно рассматривать как нераспадающиеся единые многоугольники соответственно с 5, 8 и 10 сторонами, поскольку существует непрерывный обход их вершин по сторонам вокруг центров. При этом в случае пентаграммы, например, совершая полный обход в порядке, определяемом номерами 0-5 (рис. 21), мы делаем два оборота вокруг центра пентаграммы, тогда как при обходе пятиугольника (рис. 20) мы делаем лишь один оборот. В случае же октаграммы и декаграммы получается по три 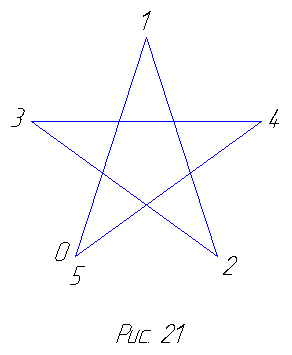 оборота вокруг центра (рис. 22 и 23). Заметим, что внутренние точки пересечения мы не рассматриваем как вершины звезды. Указанное выше обстоятельство учитывается в символических обозначениях звёздчатых многоугольников. В нашем случае пентаграмма, октаграмма и декаграмма обозначаются соответственно через 5/2, 8/3 и 10/3. Эти звёзды могут принимать, кроме того, и иные очертания,
оборота вокруг центра (рис. 22 и 23). Заметим, что внутренние точки пересечения мы не рассматриваем как вершины звезды. Указанное выше обстоятельство учитывается в символических обозначениях звёздчатых многоугольников. В нашем случае пентаграмма, октаграмма и декаграмма обозначаются соответственно через 5/2, 8/3 и 10/3. Эти звёзды могут принимать, кроме того, и иные очертания, 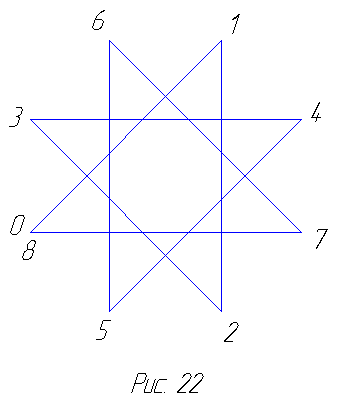 но в дальнейшем мы будем говорить лишь об описанных выше формах ([4], стр. 63 и след.).
но в дальнейшем мы будем говорить лишь об описанных выше формах ([4], стр. 63 и след.).
Если теперь обратиться к аналогичному процессу в трёхмерном пространстве, то естественно снова начать с простейшего многогранника — тетраэдра. Разумеется, здесь нам потребуется продолжить не рёбра, но грани многогранника. Однако четыре плоскости — продолжения граней тетраэдра — ограничивают лишь ту часть трёхмерного пространства, которая совпадает с исходным телом. Шесть плоскостей куба попарно параллельны и взаимно перпендикулярны, подобно сторонам двумерного аналога куба — квадрата. Поэтому и в трёхмерном случае к кубу не добавляется новых частей. Но уже случай октаэдра даёт интересные результаты. Восемь плоскостей — продолжения граней октаэдра — 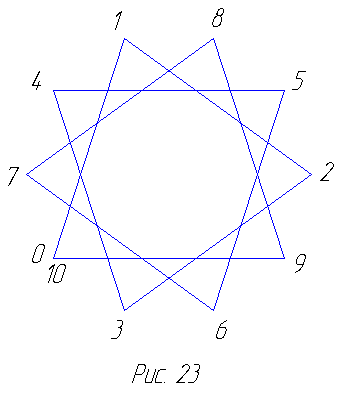 отделяют от пространства новые части, так сказать, «отсеки», внешние по отношению к октаэдру. Вы обнаружите, что эти части суть не что иное, как малые тетраэдры, основания которых совпадают с гранями октаэдра. Если вы теперь мысленно присоедините эти части к октаэдру таким образом, чтобы их общие с октаэдром грани исчезли, оставив нутро нового тела полым, перед вашим взором возникнет невыпуклый многогранник.
отделяют от пространства новые части, так сказать, «отсеки», внешние по отношению к октаэдру. Вы обнаружите, что эти части суть не что иное, как малые тетраэдры, основания которых совпадают с гранями октаэдра. Если вы теперь мысленно присоедините эти части к октаэдру таким образом, чтобы их общие с октаэдром грани исчезли, оставив нутро нового тела полым, перед вашим взором возникнет невыпуклый многогранник.
Однако с таким же успехом вы можете представить себе этот многогранник и в виде множества пересекающихся треугольных граней, вершины которых совпадают с вершинами малых тетраэдров. Эти треугольные грани обладают свойством, отмеченным у выпуклых многогранников, а именно: каждое ребро этих треугольников принадлежит в точности двум таким граням: Разумеется, эти рёбра пересекаются, но внутренние точки пересечения этих отрезков не следует рассматривать в качестве вершин многогранника, подобно тому как мы поступали в случае плоских звёздчатых многогранников. Ведь и там каждая сторона, например пентаграммы, пересекалась двумя другими, но точки их пересечения не рассматриваются как делящие сторону. Подобным же образом в звёздчатом октаэдре мы находим лишь восемь граней, и только концы рёбер считаем вершинами многогранника.
Впрочем, дальнейшее тщательное изучение наводит нас на мысль о том, что этот многогранник на самом деле есть не единое тело, но соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра, причём эта точка является центром симметрии всего тела. Этот многогранник открыл Кеплер в 1619 году и дал ему имя stella octangula1
Ещё одна особенность этого тела заключается в том, что восемь его вершин лежат в вершинах некоторого куба, а рёбра являются диагоналями граней этого куба.
Продолжать дальше грани октаэдра не имеет смысла, ибо они не отделят более никакой части пространства, не создадут новых «отсеков». Поэтому октаэдр имеет лишь о д н у звёздчатую форму.
Если же обратиться к додекаэдру, продолжив его грани как и в случае октаэдра, можно обнаружить, что это приведет к образованию т р ё х различных типов отсеков. Вблизи самого додекаэдра имеется 12 пятиугольных пирамид. Эти пирамиды превращают додекаэдр в малый звёздчатый додекаэдр. За ними следуют 30 клинообразных отсеков, превращающих малый звёздчатый додекаэдр в большой додекаэдр. Наконец 20 треугольных бипирамид2 превращают большой додекаэдр в большой звёздчатый додекаэдр, который, пожалуй, точнее было бы назвать звёздчатым большим додекаэдром. Это завершающая звёздчатая форма додекаэдра, который имеет три такие формы: две из них были открыты Кеплером (1619), третья — Пуансо (1809).
 Теперь вас, возможно, заинтересует то обстоятельство, что в отличие от октаэдра любая из звёздчатых форм додекаэдра н е я в л я е т с я соединением платоновых тел, но образует новый многогранник. На самом деле эти многогранники правильные, поскольку два из них имеют гранями по 12 пересекающихся пентаграмм, а грани третьего — 12 пересекающихся пятиугольников (пентагонов). Коши (1811) доказал, что эти три многогранника, открытые ранее, на самом деле не что иное, как звёздчатые формы додекаэдра [24]. Он также установил, что вместе с большим икосаэдром — звёздчатой формой икосаэдра — они являются единственно возможными правильными звёздчатыми телами. Так, к пяти правильным телам, известным ещё древним учёным, математики более близкой к нам эпохи добавили четыре звёздчатых многогранника, гранями которых могут быть правильные или звёздчатые многоугольники. По-прежнему грани соединяются попарно в рёбрах, но до этого они пересекаются с другими гранями. При этом внутренние линии пересечения не считаются рёбрами. Все эти свойства отчётливо прослеживаются на моделях звёздчатых тел.
Теперь вас, возможно, заинтересует то обстоятельство, что в отличие от октаэдра любая из звёздчатых форм додекаэдра н е я в л я е т с я соединением платоновых тел, но образует новый многогранник. На самом деле эти многогранники правильные, поскольку два из них имеют гранями по 12 пересекающихся пентаграмм, а грани третьего — 12 пересекающихся пятиугольников (пентагонов). Коши (1811) доказал, что эти три многогранника, открытые ранее, на самом деле не что иное, как звёздчатые формы додекаэдра [24]. Он также установил, что вместе с большим икосаэдром — звёздчатой формой икосаэдра — они являются единственно возможными правильными звёздчатыми телами. Так, к пяти правильным телам, известным ещё древним учёным, математики более близкой к нам эпохи добавили четыре звёздчатых многогранника, гранями которых могут быть правильные или звёздчатые многоугольники. По-прежнему грани соединяются попарно в рёбрах, но до этого они пересекаются с другими гранями. При этом внутренние линии пересечения не считаются рёбрами. Все эти свойства отчётливо прослеживаются на моделях звёздчатых тел.
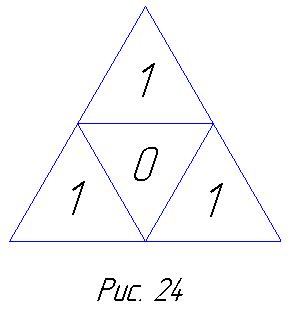
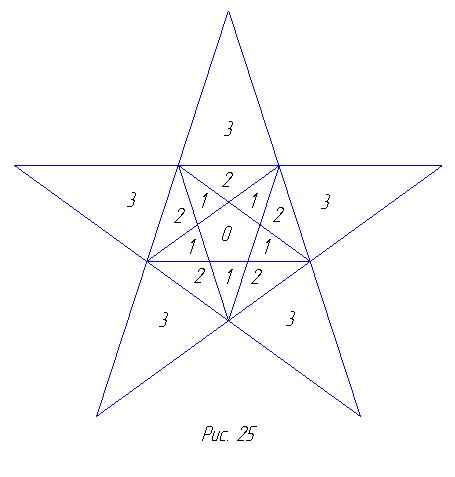 Перед построением этих моделей небезынтересно ознакомиться с устройством трафаретов, задающих какую-либо одну лицевую звёздчатую грань. Остальные грани имеют аналогичное строение. Трафаретом для октаэдра будет служить равносторонний треугольник, из которого следует вырезать треугольник с вершинами в серединах сторон (рис. 24). Этот внутренний треугольник является гранью исходного октаэдра, вне которого расположена stella octangula. Трафаретом для додекаэдра служит звёздчатый многоугольник без вырезанного звёздчатого многоугольника (рис. 25). Нумерация показывает, какие части образуют внешние по отношению к граням куски. С помощью таких трафаретов вы сможете сделать заготовки, необходимые для изготовления моделей.
Перед построением этих моделей небезынтересно ознакомиться с устройством трафаретов, задающих какую-либо одну лицевую звёздчатую грань. Остальные грани имеют аналогичное строение. Трафаретом для октаэдра будет служить равносторонний треугольник, из которого следует вырезать треугольник с вершинами в серединах сторон (рис. 24). Этот внутренний треугольник является гранью исходного октаэдра, вне которого расположена stella octangula. Трафаретом для додекаэдра служит звёздчатый многоугольник без вырезанного звёздчатого многоугольника (рис. 25). Нумерация показывает, какие части образуют внешние по отношению к граням куски. С помощью таких трафаретов вы сможете сделать заготовки, необходимые для изготовления моделей.
На следующих страницах светлой штриховкой обозначены те части граней, которые видны с соответствующих вершин многогранника, лежащих над рассматриваемой гранью. Чёрным цветом показана часть этой же звёздчатой грани, видимая с противоположной стороны. По всем выделенным частям мы получаем возможность судить, какими должны быть заготовки для той или иной модели.
1 Stella octangula (лат.) — восьмиугольная звезда.
2 Бипирамидой называется многогранник, образованный из двух n-угольных пирамид, которые сложены равными основаниями (и находятся по разные стороны от общего основания).
<—
Часть 2
—>

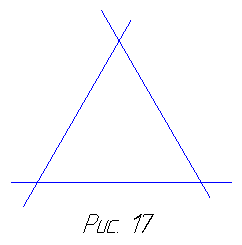
 Начнём с простейшего многоугольника — равностороннего треугольника. Посмотрим, что произойдёт, если мы продолжим все три его стороны. Легко заметить, что этими прямыми не будет ограничена никакая новая часть плоскости: продолжения сторон будут р а с х о д и т ь с я (рис. 17). Аналогичная картина предстанет перед нами и в том случае, если мы попытаемся продолжить стороны квадрата. Построенные прямые будут попарно параллельны и не пересекутся, сколько бы их ни продолжали (рис. 18). Тем самым они не добавят никаких новых ограниченных частей плоскости к внутренности квадрата. Однако в случае пятиугольника картина меняется. Продолжения сторон пятиугольника пересекаются во внешней по отношению к пятиугольнику части плоскости, добавляя к пятиугольнику новые части. В результате получается хорошо известная нам пятиконечная звезда, иначе называемая пентаграммой (рис. 19). Пентаграмма была известна в
Начнём с простейшего многоугольника — равностороннего треугольника. Посмотрим, что произойдёт, если мы продолжим все три его стороны. Легко заметить, что этими прямыми не будет ограничена никакая новая часть плоскости: продолжения сторон будут р а с х о д и т ь с я (рис. 17). Аналогичная картина предстанет перед нами и в том случае, если мы попытаемся продолжить стороны квадрата. Построенные прямые будут попарно параллельны и не пересекутся, сколько бы их ни продолжали (рис. 18). Тем самым они не добавят никаких новых ограниченных частей плоскости к внутренности квадрата. Однако в случае пятиугольника картина меняется. Продолжения сторон пятиугольника пересекаются во внешней по отношению к пятиугольнику части плоскости, добавляя к пятиугольнику новые части. В результате получается хорошо известная нам пятиконечная звезда, иначе называемая пентаграммой (рис. 19). Пентаграмма была известна в 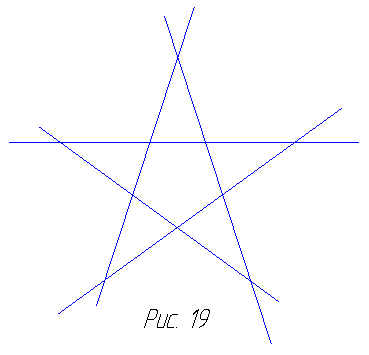 глубокой древности, что явствует хотя бы из того, что пифагорейцы считали её символом здоровья. Продолжение сторон шестиугольника приводит к появлению шестиугольной звезды, или гексаграммы (последнюю можно рассматривать не как единый многоугольник, а как соединение двух равносторонних треугольников).
глубокой древности, что явствует хотя бы из того, что пифагорейцы считали её символом здоровья. Продолжение сторон шестиугольника приводит к появлению шестиугольной звезды, или гексаграммы (последнюю можно рассматривать не как единый многоугольник, а как соединение двух равносторонних треугольников). Аналогично правильный восьмиугольник (октагон) приводит нас к восьмиугольной звезде — октаграмме, правильный десятиугольник (декагон) — к десятиугольной звезде, или декаграмме. Пентаграмму, октаграмму и декаграмму можно рассматривать как нераспадающиеся единые многоугольники соответственно с 5, 8 и 10 сторонами, поскольку существует непрерывный обход их вершин по сторонам вокруг центров. При этом в случае пентаграммы, например, совершая полный обход в порядке, определяемом номерами 0-5 (рис. 21
Аналогично правильный восьмиугольник (октагон) приводит нас к восьмиугольной звезде — октаграмме, правильный десятиугольник (декагон) — к десятиугольной звезде, или декаграмме. Пентаграмму, октаграмму и декаграмму можно рассматривать как нераспадающиеся единые многоугольники соответственно с 5, 8 и 10 сторонами, поскольку существует непрерывный обход их вершин по сторонам вокруг центров. При этом в случае пентаграммы, например, совершая полный обход в порядке, определяемом номерами 0-5 (рис. 21 оборота вокруг центра (рис. 22 и 23
оборота вокруг центра (рис. 22 и 23 но в дальнейшем мы будем говорить лишь об описанных выше формах ([4], стр. 63 и след.).
но в дальнейшем мы будем говорить лишь об описанных выше формах ([4], стр. 63 и след.).
 отделяют от пространства новые части, так сказать, «отсеки», внешние по отношению к октаэдру. Вы обнаружите, что эти части суть не что иное, как малые тетраэдры, основания которых совпадают с гранями октаэдра. Если вы теперь мысленно присоедините эти части к октаэдру таким образом, чтобы их общие с октаэдром грани исчезли, оставив нутро нового тела полым, перед вашим взором возникнет невыпуклый многогранник.
отделяют от пространства новые части, так сказать, «отсеки», внешние по отношению к октаэдру. Вы обнаружите, что эти части суть не что иное, как малые тетраэдры, основания которых совпадают с гранями октаэдра. Если вы теперь мысленно присоедините эти части к октаэдру таким образом, чтобы их общие с октаэдром грани исчезли, оставив нутро нового тела полым, перед вашим взором возникнет невыпуклый многогранник. Теперь вас, возможно, заинтересует то обстоятельство, что в отличие от октаэдра любая из звёздчатых форм додекаэдра н е я в л я е т с я соединением платоновых тел, но образует новый многогранник. На самом деле эти многогранники правильные, поскольку два из них имеют гранями по 12 пересекающихся пентаграмм, а грани третьего — 12 пересекающихся пятиугольников (пентагонов). Коши (1811) доказал, что эти три многогранника, открытые ранее, на самом деле не что иное, как звёздчатые формы додекаэдра [24]. Он также установил, что вместе с большим икосаэдром — звёздчатой формой икосаэдра — они являются единственно возможными правильными звёздчатыми телами. Так, к пяти правильным телам, известным ещё древним учёным, математики более близкой к нам эпохи добавили четыре звёздчатых многогранника, гранями которых могут быть правильные или звёздчатые многоугольники. По-прежнему грани соединяются попарно в рёбрах, но до этого они пересекаются с другими гранями. При этом внутренние линии пересечения не считаются рёбрами. Все эти свойства отчётливо прослеживаются на моделях звёздчатых тел.
Теперь вас, возможно, заинтересует то обстоятельство, что в отличие от октаэдра любая из звёздчатых форм додекаэдра н е я в л я е т с я соединением платоновых тел, но образует новый многогранник. На самом деле эти многогранники правильные, поскольку два из них имеют гранями по 12 пересекающихся пентаграмм, а грани третьего — 12 пересекающихся пятиугольников (пентагонов). Коши (1811) доказал, что эти три многогранника, открытые ранее, на самом деле не что иное, как звёздчатые формы додекаэдра [24]. Он также установил, что вместе с большим икосаэдром — звёздчатой формой икосаэдра — они являются единственно возможными правильными звёздчатыми телами. Так, к пяти правильным телам, известным ещё древним учёным, математики более близкой к нам эпохи добавили четыре звёздчатых многогранника, гранями которых могут быть правильные или звёздчатые многоугольники. По-прежнему грани соединяются попарно в рёбрах, но до этого они пересекаются с другими гранями. При этом внутренние линии пересечения не считаются рёбрами. Все эти свойства отчётливо прослеживаются на моделях звёздчатых тел. Перед построением этих моделей небезынтересно ознакомиться с устройством трафаретов, задающих какую-либо одну лицевую звёздчатую грань. Остальные грани имеют аналогичное строение. Трафаретом для октаэдра будет служить равносторонний треугольник, из которого следует вырезать треугольник с вершинами в серединах сторон (рис. 24
Перед построением этих моделей небезынтересно ознакомиться с устройством трафаретов, задающих какую-либо одну лицевую звёздчатую грань. Остальные грани имеют аналогичное строение. Трафаретом для октаэдра будет служить равносторонний треугольник, из которого следует вырезать треугольник с вершинами в серединах сторон (рис. 24