Математическая классификация
(при первом чтении этот раздел можно опустить)
Любой однородный многогранник можно поместить внутри сферы таким образом, что его оси симметрии пройдут через центр сферы. Спроектировав затем из центра на поверхность сферы рёбра многогранника, мы получим сеть, состоящую из дуг больших окружностей сферы. Эта сеть разбивает сферу на сферические многоугольники, каждый из которых соответствует одной грани многогранника. Плоскости симметрии многогранника добавят к разбиению новые дуги, так что если исходный многогранник, к примеру, был платоновым телом, то с учётом новых дуг поверхность сферы будет разделена на сферические треугольники — по четыре для каждого ребра.
Эти сферические треугольники получили название треугольников Мёбиуса, по имени впервые рассмотревшего их математика (1849). Мёбиус же первым применил идею этих треугольников к устройству многогранного калейдоскопа, который составлен из трёх зеркал, образующих трёхгранный угол. Внося в такой калейдоскоп какое-либо тело, изображающее материальную точку, мы, глядя на неё и её отражения в двух зеркалах, увидим вершины соответствующего многогранника. Другой, возможно, более простой иллюстрацией треугольников Мёбиуса является соответствующая сеть линий, нанесённых мелом на чёрном глобусе, на котором хорошо видны проведённые линии1. При этом определённые точки пересечения больших кругов сферы будут соответствовать вершинам многогранника. Полученная решётчатая сеть сферических треугольников покрывает глобус однократно. Все треугольники сети конгруэнтны, то есть равны между собой.
Каждый из этих треугольников можно обозначить символом (pqr), где р, q и r — натуральные числа, соответственно равные знаменателям дробей π/р, π/q и π/r, выражающих радианные меры углов треугольника. В нашем случае р, q и r могут принимать лишь целые значения 2, 3, 4 или 5. Если позволить р, q и r принимать дробные значения, то для определённых наборов дробей мы снова получим сеть треугольников с соответствующими углами. Эти треугольники носят имя Г. А. Шварца, который первым указал все возможные здесь случаи (1873). Было показано, что множество треугольников Шварца также покрывает глобус, но не однократно, а некоторое конечное число раз, так что оно в определённом смысле эквивалентно множеству треугольников Мёбиуса. Поэтому треугольники Шварца можно классифицировать как тетраэдральные, октаэдральные или икосаэдральные в зависимости от того, с какими треугольниками Мёбиуса они соотносятся (см. [15, 16, 18]).
Эти идеи можно сделать наглядными, используя подходящие модели. Прежде всего вы можете изготовить многогранный калейдоскоп из трёх зеркал, вырезанных в форме кругового сектора. Радиус секторов следует взять довольно большим — порядка 30 см или больше; центральные углы секторов должны содержать:
для тетраэдрального калейдоскопа 54°44', 54°44', 70°32';
для октаэдрального калейдоскопа 35°16', 45°, 54°44';
для икосаэдрального калейдоскопа 20°54', 31°43', 37°23'.
Хотя такие калейдоскопы достаточно трудны в изготовлении, игра с ними доставляет истинное удовольствие.
Столь же (а быть может, и в большей мере) поучительно изготовить модели этих сферических треугольников из плотной бумаги или картона. Присоединяя один к другому требуемое число таких треугольников, вы получите модель сферы в виде множества пересекающих её больших кругов. Можно, конечно, раскрасить большие круги по-разному, но это слишком усложнит работу.
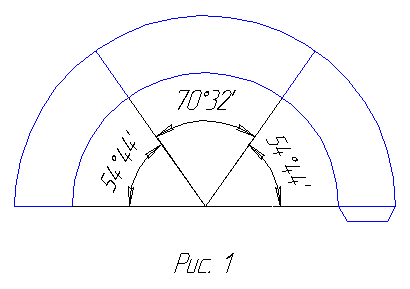
 Проще всего начать с тетраэдрального треугольника. Заготовка для вырезания
показана на рис. 1.
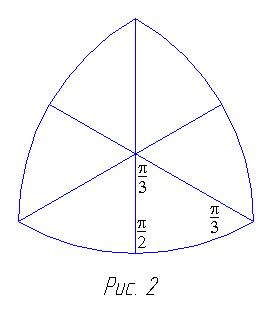
Перегните заготовку по радиальным линиям и придайте ей форму сферического треугольника. Модель скрепляется клеем всего в одном месте при помощи наклейки, видной на рисун-ке. Надо сделать 24 одинаковые модели и склеить их плоскими частями таким образом, чтобы наклейки были не видны. Эту работу можно выполнять по частям. Одну такую часть составляют шесть сфе-рических треугольников, склеенных меж-ду собой так, как показано на рис. 2.
Их углы равны π/2, π/З и π/3. Четыре части образуют модель сферы.
Проще всего начать с тетраэдрального треугольника. Заготовка для вырезания
показана на рис. 1.
Перегните заготовку по радиальным линиям и придайте ей форму сферического треугольника. Модель скрепляется клеем всего в одном месте при помощи наклейки, видной на рисун-ке. Надо сделать 24 одинаковые модели и склеить их плоскими частями таким образом, чтобы наклейки были не видны. Эту работу можно выполнять по частям. Одну такую часть составляют шесть сфе-рических треугольников, склеенных меж-ду собой так, как показано на рис. 2.
Их углы равны π/2, π/З и π/3. Четыре части образуют модель сферы.
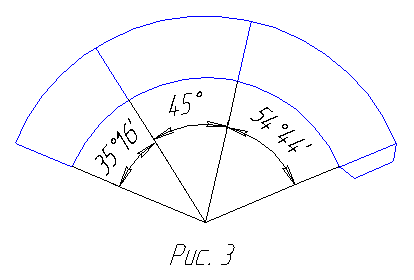
 Для октаэдральных треугольников после-довательность действий аналогична; ис-ходная заготовка показана на рис. 3.
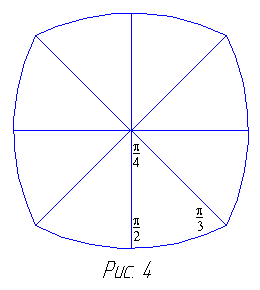
Вам потребуется 48 октаэдральных треугольни-ков, образующих два энантиоморфных множества по 24 в каждом. Можно взять заготовки любого подходящего для вас раз-мера. Можно также по желанию делать кольцо шире или ýже. Можно даже оста-вить всю внутренность секторов, ничего не вырезая, и тогда на модели сферы будет точно указан её центр. При склеивании частей модели начинает обнаруживаться феномен двойственности октаэдра и куба, поскольку каждая из этих частей может быть составлена из восьми сферических треугольников, расположенных в порядке, показанном
на рис. 4.
Их углы равны π/2, π/З и π/4. Шесть таких частей образуют модель сферы.
Для октаэдральных треугольников после-довательность действий аналогична; ис-ходная заготовка показана на рис. 3.
Вам потребуется 48 октаэдральных треугольни-ков, образующих два энантиоморфных множества по 24 в каждом. Можно взять заготовки любого подходящего для вас раз-мера. Можно также по желанию делать кольцо шире или ýже. Можно даже оста-вить всю внутренность секторов, ничего не вырезая, и тогда на модели сферы будет точно указан её центр. При склеивании частей модели начинает обнаруживаться феномен двойственности октаэдра и куба, поскольку каждая из этих частей может быть составлена из восьми сферических треугольников, расположенных в порядке, показанном
на рис. 4.
Их углы равны π/2, π/З и π/4. Шесть таких частей образуют модель сферы.
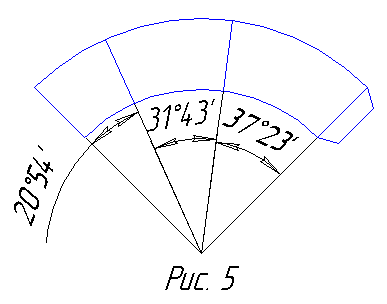
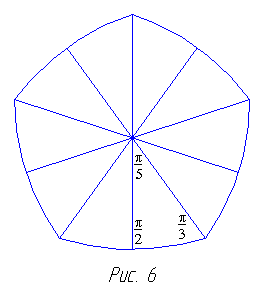 Икосаэдральные треугольники более трудоём-ки в изготовлении из-за большого числа заго-товок, но последовательность действий оста-ётся той же. Как нам кажется, целесообразно приложить усилия, ибо результат весьма поу-чителен: на этой модели по сравнению с пре-дыдущими очень явно прослеживается её внутреннее строение. Вам потребуется 120 за-готовок (рис. 5), образующих два энантио-морфных множества по 60 заготовок в каж-дом. На сей раз части будут пятиугольными, содержащими по десять сферических треуголь-ников (рис. 6). Их углы будут равны π/2, π/З и π/5. Двенадцать таких частей образуют модель сферы.
Икосаэдральные треугольники более трудоём-ки в изготовлении из-за большого числа заго-товок, но последовательность действий оста-ётся той же. Как нам кажется, целесообразно приложить усилия, ибо результат весьма поу-чителен: на этой модели по сравнению с пре-дыдущими очень явно прослеживается её внутреннее строение. Вам потребуется 120 за-готовок (рис. 5), образующих два энантио-морфных множества по 60 заготовок в каж-дом. На сей раз части будут пятиугольными, содержащими по десять сферических треуголь-ников (рис. 6). Их углы будут равны π/2, π/З и π/5. Двенадцать таких частей образуют модель сферы.
Существует ещё один способ изготовления моделей, иллюстрирующих треугольники Мёбиуса. Он сводится к построению модели такого многогранника с плоскими треугольными гранями, вершины которого совпадали бы с вершинами сферических треугольников. Если стороны сферического треугольника равны р, q и r (точнее, р, q и r суть центральные углы сферы, опирающиеся на эти дуги), то соответствующие стороны плоского треугольника должны находиться в отношении, равном
sin(р/2) : sin(q/2) : sin(r/2).
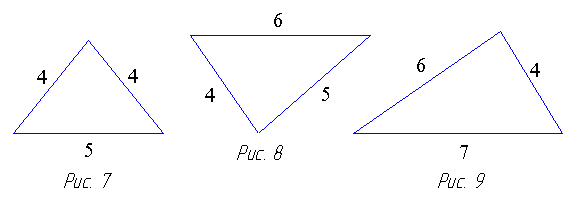 Соответствующие треугольники для трёх разобранных выше случаев показаны на рис. 7-9. Разумеется, в каждом таком случае нужное число плоских треугольников равно числу сферических треугольников. Эти модели можно клеить, придерживаясь той же схемы разбиения на части, что и разобранные выше. Числа, проставленные на ри-сунках, дают приближённые значения линейных размеров соответствующих плоских треугольников. В качестве ли-нейного масштаба можно взять 1 см; в этом случае вы придёте к вполне удовлетворительным результатам.
Соответствующие треугольники для трёх разобранных выше случаев показаны на рис. 7-9. Разумеется, в каждом таком случае нужное число плоских треугольников равно числу сферических треугольников. Эти модели можно клеить, придерживаясь той же схемы разбиения на части, что и разобранные выше. Числа, проставленные на ри-сунках, дают приближённые значения линейных размеров соответствующих плоских треугольников. В качестве ли-нейного масштаба можно взять 1 см; в этом случае вы придёте к вполне удовлетворительным результатам.
Сделав некоторые треугольники белыми, а остальные раскрасив в другие цвета, вы добьётесь
красивого
цветового
эффекта.
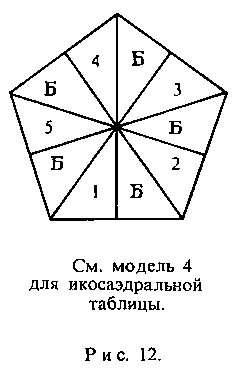
На рис. 10-12 показаны нужные части; внизу приведены таблицы их раскраски.
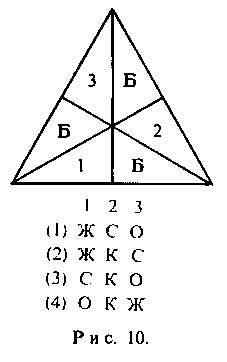
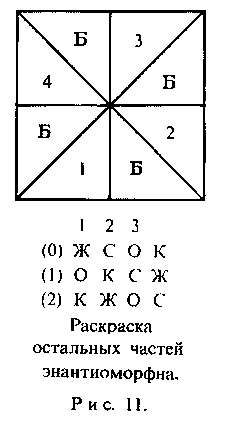
 Заметим, что в тетраэдральном случае у нас имеются четыре части, которые обозначены на таблицах через (1), (2), (3) и (4). В остальных двух случаях нет нужды приводить полные таблицы раскраски для всех частей. Это объяс-няется тем, что тетраэдр и усечённый тетраэдр — единственные однород-ные многогранники, вершины кото-рых н е р а з б и в а ю т с я на диаметрально противоположные па-ры. В остальных двух случаях центр части (0) условимся считать северным полюсом модели. В октаэдральной мо-дели затем приклеиваются на свои места части (1) и (2), образуя нечто вроде граней куба. За ними следуют энантиоморфные аналоги этих же час-тей, образуя тем самым как бы боковые грани куба. Энантиоморфный аналог части (0) завершает эту модель.
Заметим, что в тетраэдральном случае у нас имеются четыре части, которые обозначены на таблицах через (1), (2), (3) и (4). В остальных двух случаях нет нужды приводить полные таблицы раскраски для всех частей. Это объяс-няется тем, что тетраэдр и усечённый тетраэдр — единственные однород-ные многогранники, вершины кото-рых н е р а з б и в а ю т с я на диаметрально противоположные па-ры. В остальных двух случаях центр части (0) условимся считать северным полюсом модели. В октаэдральной мо-дели затем приклеиваются на свои места части (1) и (2), образуя нечто вроде граней куба. За ними следуют энантиоморфные аналоги этих же час-тей, образуя тем самым как бы боковые грани куба. Энантиоморфный аналог части (0) завершает эту модель.
Наиболее интересен случай икосаэдра. Вы снова начинаете с части (0): склеиваете вместе десять треугольников, чередуя белые с треугольниками других цветов в соответствии с таблицей раскраски икосаэдра. Затем подготавливаете части (1), (2), (3), (4) и (5) и приклеиваете их к части (0) по очереди, строя таким образом фигуру, напоминающую додекаэдр. Следующие шесть частей имеют энантиоморфный порядок раскраски и располагаются диаметрально противоположно своим двойникам.
Идеальная симметрия раскраски во всех трёх моделях приведёт вас в восхищение, но особенно впечатляет последняя. Здесь стоит упомянуть ещё и о том, что три наших многогранника д в о й с т в е н н ы архимедовым телам. Двойственными называются такие многогранники, которые имеют одно и то же число рёбер, но при этом число граней одного равно числу вершин другого и, наоборот, число вершин одного равно числу граней другого. Кроме того, n-сторонней грани в одном из них соответствует вершина другого, в которой сходятся n рёбер. Только что построенные нами многогранники двойственны многогранникам, помещённым в книге под номерами 7, 15 и 16 соответственно.
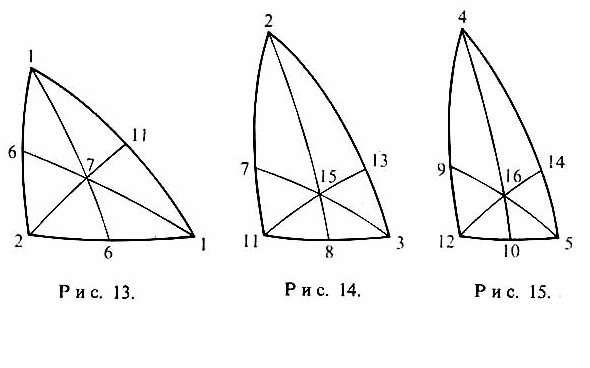 Теперь, если вы сделали разобранные модели, их можно использовать для того, чтобы определить, как располо-жены вершины, рёбра и грани выпуклых однородных многогранников. Это отличная тренировка простран-ственного воображения. Лучше всего использовать для этой цели сферические модели. Большую помощь ока-жут приведённые диаграммы
(рис. 13-15), изображаю-щие соответственные сферические треугольники наших трёх моделей. Вершины диаграмм указывают характер-ные точки сферических треугольников соответствующей модели. При этом числа, стоящие у вершин, указывают, вершиной какого многогранника на модели является та или иная точка. Соответствующие номера приводятся в сводном списке выпуклых однородных многогранни-ков2. На диаграммах не указаны номера моделей «кур-носых» тел 17 и 18. Вершины этих тел находятся более сложным способом, описание которого можно найти в специальной литературе (см., например, L. L i n e s, Solid Geometry, N.Y., Dover Publ., 1965).
Теперь, если вы сделали разобранные модели, их можно использовать для того, чтобы определить, как располо-жены вершины, рёбра и грани выпуклых однородных многогранников. Это отличная тренировка простран-ственного воображения. Лучше всего использовать для этой цели сферические модели. Большую помощь ока-жут приведённые диаграммы
(рис. 13-15), изображаю-щие соответственные сферические треугольники наших трёх моделей. Вершины диаграмм указывают характер-ные точки сферических треугольников соответствующей модели. При этом числа, стоящие у вершин, указывают, вершиной какого многогранника на модели является та или иная точка. Соответствующие номера приводятся в сводном списке выпуклых однородных многогранни-ков2. На диаграммах не указаны номера моделей «кур-носых» тел 17 и 18. Вершины этих тел находятся более сложным способом, описание которого можно найти в специальной литературе (см., например, L. L i n e s, Solid Geometry, N.Y., Dover Publ., 1965).
1 Такие глобусы выпускаются в Англии как учебные пособия для классных занятий географией и астрономией.
2 Так, под номером 12 в списке помещён икосододекаэдр. Мы можем найти этот номер на диаграмме рис. 15, изображающей сферический треугольник для третьей икосаэдральной сферической модели. Из диаграмм видно, что этим номером обозначена вершина прямого угла сфе-рического треугольника. Следовательно, вершины прямых углов всех сферических треугольников этой модели являются вершинами икосодо-декаэдра.
<—
Содержание
—>


 Проще всего начать с тетраэдрального треугольника. Заготовка для вырезания
показана на рис. 1.
Перегните заготовку по радиальным линиям и придайте ей форму сферического треугольника. Модель скрепляется клеем всего в одном месте при помощи наклейки, видной на рисун-ке. Надо сделать 24 одинаковые модели и склеить их плоскими частями таким образом, чтобы наклейки были не видны. Эту работу можно выполнять по частям. Одну такую часть составляют шесть сфе-рических треугольников, склеенных меж-ду собой так, как показано на рис. 2.
Их углы равны π/2, π/З и π/3. Четыре части образуют модель сферы.
Проще всего начать с тетраэдрального треугольника. Заготовка для вырезания
показана на рис. 1.
Перегните заготовку по радиальным линиям и придайте ей форму сферического треугольника. Модель скрепляется клеем всего в одном месте при помощи наклейки, видной на рисун-ке. Надо сделать 24 одинаковые модели и склеить их плоскими частями таким образом, чтобы наклейки были не видны. Эту работу можно выполнять по частям. Одну такую часть составляют шесть сфе-рических треугольников, склеенных меж-ду собой так, как показано на рис. 2.
Их углы равны π/2, π/З и π/3. Четыре части образуют модель сферы.
 Для октаэдральных треугольников после-довательность действий аналогична; ис-ходная заготовка показана на
Для октаэдральных треугольников после-довательность действий аналогична; ис-ходная заготовка показана на 
 Икосаэдральные треугольники более трудоём-ки в изготовлении из-за большого числа заго-товок, но последовательность действий оста-ётся той же. Как нам кажется, целесообразно приложить усилия, ибо результат весьма поу-чителен: на этой модели по сравнению с пре-дыдущими очень явно прослеживается её внутреннее строение. Вам потребуется 120 за-готовок (
Икосаэдральные треугольники более трудоём-ки в изготовлении из-за большого числа заго-товок, но последовательность действий оста-ётся той же. Как нам кажется, целесообразно приложить усилия, ибо результат весьма поу-чителен: на этой модели по сравнению с пре-дыдущими очень явно прослеживается её внутреннее строение. Вам потребуется 120 за-готовок ( Соответствующие треугольники для трёх разобранных выше случаев показаны на
Соответствующие треугольники для трёх разобранных выше случаев показаны на 

 Заметим, что в тетраэдральном случае у нас имеются четыре части, которые обозначены на таблицах через (1), (2), (3) и (4). В остальных двух случаях нет нужды приводить полные таблицы раскраски для всех частей. Это объяс-няется тем, что тетраэдр и усечённый тетраэдр — единственные однород-ные многогранники, вершины кото-рых н е р а з б и в а ю т с я на диаметрально противоположные па-ры. В остальных двух случаях центр части (0) условимся считать северным полюсом модели. В октаэдральной мо-дели затем приклеиваются на свои места части (1) и (2), образуя нечто вроде граней куба. За ними следуют энантиоморфные аналоги этих же час-тей, образуя тем самым как бы боковые грани куба. Энантиоморфный аналог части (0) завершает эту модель.
Заметим, что в тетраэдральном случае у нас имеются четыре части, которые обозначены на таблицах через (1), (2), (3) и (4). В остальных двух случаях нет нужды приводить полные таблицы раскраски для всех частей. Это объяс-няется тем, что тетраэдр и усечённый тетраэдр — единственные однород-ные многогранники, вершины кото-рых н е р а з б и в а ю т с я на диаметрально противоположные па-ры. В остальных двух случаях центр части (0) условимся считать северным полюсом модели. В октаэдральной мо-дели затем приклеиваются на свои места части (1) и (2), образуя нечто вроде граней куба. За ними следуют энантиоморфные аналоги этих же час-тей, образуя тем самым как бы боковые грани куба. Энантиоморфный аналог части (0) завершает эту модель. Теперь, если вы сделали разобранные модели, их можно использовать для того, чтобы определить, как располо-жены вершины, рёбра и грани выпуклых однородных многогранников. Это отличная тренировка простран-ственного воображения. Лучше всего использовать для этой цели сферические модели. Большую помощь ока-жут приведённые диаграммы
(рис. 13-15), изображаю-щие соответственные сферические треугольники наших трёх моделей. Вершины диаграмм указывают характер-ные точки сферических треугольников соответствующей модели. При этом числа, стоящие у вершин, указывают, вершиной какого многогранника на модели является та или иная точка. Соответствующие номера приводятся в сводном списке выпуклых однородных многогранни-ков
Теперь, если вы сделали разобранные модели, их можно использовать для того, чтобы определить, как располо-жены вершины, рёбра и грани выпуклых однородных многогранников. Это отличная тренировка простран-ственного воображения. Лучше всего использовать для этой цели сферические модели. Большую помощь ока-жут приведённые диаграммы
(рис. 13-15), изображаю-щие соответственные сферические треугольники наших трёх моделей. Вершины диаграмм указывают характер-ные точки сферических треугольников соответствующей модели. При этом числа, стоящие у вершин, указывают, вершиной какого многогранника на модели является та или иная точка. Соответствующие номера приводятся в сводном списке выпуклых однородных многогранни-ков