Надо полагать, теперь вы достаточно уяснили процесс, посредством которого получаются звёздчатые формы многогранников. Некоторые из них суть соединения нескольких тел. До сих пор нам пришлось встретиться лишь с одним таким соединением — звёздчатым октаэдром. Больше подобных форм мы найдём, рассматривая икосаэдр. Все три звёздчатые формы додекаэдра представляют собой единые и нерасчленяемые новые многогранники, которым находится место в классификации правильных тел.

Икосаэдр имеет двадцать граней. Если каждую из них продолжить неограниченно, то тело будет окружено великим многоообразием отсеков — частей пространства, ограниченных плоскостями граней. Вы, конечно, можете попытаться их себе представить, но скорее всего потерпите неудачу. Все звёздчатые формы икосаэдра можно получить добавлением к исходному телу таких отсеков. Не считая самого икосаэдра, продолжения его граней отделяют от пространства

20 + 30 + 60 + 20 + 60 + 120 + 12 + 30 + 60 + 60

отсеков десяти различных форм и размеров. Большой икосаэдр состоит из всех этих кусков, за исключением последних шестидесяти. При построении модели здесь, как и в случаях октаэдра и додекаэдра, можно пойти по следующему пути: сначала сделать модели дополнительных отсеков (предварительно запасясь необходимыми заготовками), а затем подклеить их либо к исходному многогранному основанию, либо друг к другу. Правда, на практике такой способ весьма утомителен и к тому же не даёт сколько-нибудь удовлетворительных результатов. (Тем не менее в целях разработки удобных и практичных заготовок весьма полезно представлять себе формы и вид дополнительных отсеков.) В последующих описаниях вы найдёте чертежи, по которым можно сделать нужные заготовки. Как только вы построите ту или иную модель, а ещё лучше — все модели этого раздела, что, конечно, потребует времени, вам нетрудно будет найти и другие способы изготовления моделей, требующие исходных заготовок иных форм и видов. Заготовки, приводимые ниже, вовсе не единственно возможные или самые лучшие — просто мы сочли нужным описать те из них, которые были использованы при изготовлении показанных на фотографиях моделей.

Среди звёздчатых форм икосаэдра встречаются некоторые соединения платоновых тел. Среди них: соединение пяти октаэдров, энантиоморфные формы соединения пяти тетраэдров и соединение десяти тетраэдров. Если бы Платон смог видеть эти формы, они привели бы его в восхищение. После того как были открыты эти и ряд других многогранников, учёные, естественно, задумались над вопросом: сколько существует звёздчатых форм икосаэдра? В 1900 году Брюкнер опубликовал классическую работу о многогранниках, озаглавленную "Vielecke und Vielflache" [10], в которой были представлены некоторые новые звёздчатые формы икосаэдра. Открытием ещё нескольких форм мы обязаны Уиллеру (1924). В 1938 году систематическое и полное исследование вопроса провёл Кокстер совместно с Дювалем, Флэзером и Петри [17]. Для различения исходных форм и выделения характерных тел - они применили правила ограничения, установленные Дж. Миллером.

Кокстер доказал, что существует всего 59 звёздчатых форм икосаэдра, из которых 32 обладают полной, а 27 неполной икосаэдральной симметрией (последнее обстоятельство даёт возможность строить энантиоморфные им аналоги, которые имеют красивый и необычный вид).

В высшей степени интересен трафарет, используемый для конструирования заготовок звёздчатых форм икосаэдра. Проще всего его изготовить следующим образом: возьмите один равносторонний треугольник с достаточно большой стороной. (Этот треугольник равен одной грани большого икосаэдра.) На каждой стороне треугольника следует выбрать две точки, каждая из которых делит сторону в отношении золотого сечения. Для обозначения этого отношения мы иногда будем использовать символ τ. Как известно,

τ = (1+√5)/2 ≈ 1,618.

Для нахождения нужных нам точек полезно использовать числа Фибоначчи¹

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 ...

Отношение двух соседних членов этой последовательности чисел приближённо равно «золотому сечению», ибо своим пределом это отношение имеет число τ. Удобно пользоваться линейкой с миллиметровыми делениями. Тогда части сторон треугольника могут равняться, например, 34/2, 21/2, 13/2 и 8/2 см. Отрезки, соединяющие отмеченные таким образом на сторонах точки, задают трафарет (рис. 26).

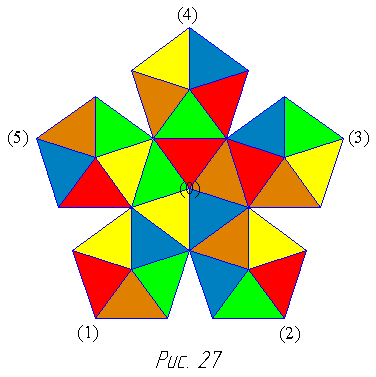На рис. 27 показано распределение цветов, подходящее для всех звёздчатых форм икосаэдра. Оно совпадает с распределением, приведённым в описании модели 4 в первой таблице раскраски. Здесь использовано пять цветов, причём каждый из них встречается вблизи любой вершины. Но порядок размещения цветов меняется от вершины к вершине. На рис. 27 пронумеровано и показано шесть вершин. Раскраска остальных шести энантиоморфна. Этот рисунок вполне заменяет таблицу раскраски, так что мы будем обращаться к нему во всех случаях, когда выполняемая модель будет обладать симметрией икосаэдра.

Возможно, вас удивит то обстоятельство, что многие звёздчатые формы икосаэдра имеют и весьма заметную симметрию додекаэдра. Объяснение этому следует искать в принципе двойственности. Икосаэдр и додекаэдр образуют двойственную пару, подобную паре октаэдр - куб. И только тетраэдр двойствен самому себе, иначе говоря, другому тетраэдру [19].