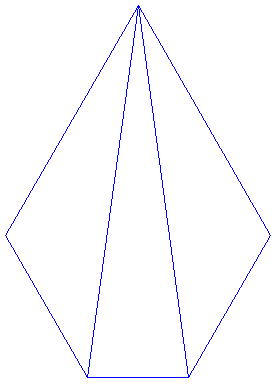Показанный на фотографии многогранник — завершающая звёздчатая форма икосаэдра¹. Модель как бы ощетинена иглами, группирующимися по пять в красивые и отчётливо заметные гроздья. Вся модель состоит из 12 таких гроздьев. Слева показана заготовка для одной части модели — трёхгранного пика. Таких заготовок потребуется ровно 60. И хотя они не обеспечивают одноцветной окраски граней звёздчатого многогранника, при желании вы можете этого добиться: нужно только склеить исходные части в такой же трёхгранный пик. Пять частей соединяются в гроздь, причём края основания грозди должны образовать правильный пятиугольник. После этого 12 гроздьев склеиваются способом, обычным для построения тел с додекаэдральной симметрией.

Обратите внимание на следующее обстоятельство: если использовать показанную слева заготовку, то по сравнению с большим икосаэдром этот многогранник будет существенно бóльшим по размерам. Так, если высота большого икосаэдра приблизительно равна 24 см, то высота рассматриваемой модели составит примерно 58 см. Поэтому, коль скоро вы не преследуете цель выяснить сравнительную величину двух моделей², уменьшите размеры трафарета. Если вы намерены воспользоваться нашим методом построения моделей и изготовить полую внутри модель, подобное уменьшение размеров заготовок придаст модели дополнительную прочность. Построенная модель на редкость красива: 60 игл, исходящих из её тела, напоминают солнечные лучи.

* * *

Если вас заинтересуют другие модели звёздчатых икосаэдров, рекомендуем воспользоваться книгой Кокстера и др. «Пятьдесят девять икосаэдров» [17]. В ней описаны всевозможные звёздчатые формы икосаэдра, проиллюстрированные великолепными чертежами самих тел и их граней. С их помощью вы сможете самостоятельно разработать типы и вид нужных заготовок. Каждый из многогранников как бы бросает вам вызов — вы сумеете победить, лишь построив его модель.